Lecture 4: Numpy and Matplotlib¶
These are two of the most fundamental parts of the scientific python "ecosystem". Most everything else is built on top of them.
To install Matplotlib:¶
Open a Terminal window, activate rcaes_env:
conda activate rcaes_env conda install -c conda-forge matplotlib
Numpy¶
In [4]:
Copied!
import numpy as np
import numpy as np
What did we just do? We imported a package. This brings new variables (mostly functions) into our interpreter. We access them as follows.
In [3]:
Copied!
# find out what's in numpy
dir(np)
# find out what's in numpy
dir(np)
Out[3]:
['ALLOW_THREADS', 'AxisError', 'BUFSIZE', 'CLIP', 'ComplexWarning', 'DataSource', 'ERR_CALL', 'ERR_DEFAULT', 'ERR_IGNORE', 'ERR_LOG', 'ERR_PRINT', 'ERR_RAISE', 'ERR_WARN', 'FLOATING_POINT_SUPPORT', 'FPE_DIVIDEBYZERO', 'FPE_INVALID', 'FPE_OVERFLOW', 'FPE_UNDERFLOW', 'False_', 'Inf', 'Infinity', 'MAXDIMS', 'MAY_SHARE_BOUNDS', 'MAY_SHARE_EXACT', 'MachAr', 'ModuleDeprecationWarning', 'NAN', 'NINF', 'NZERO', 'NaN', 'PINF', 'PZERO', 'PackageLoader', 'RAISE', 'RankWarning', 'SHIFT_DIVIDEBYZERO', 'SHIFT_INVALID', 'SHIFT_OVERFLOW', 'SHIFT_UNDERFLOW', 'ScalarType', 'Tester', 'TooHardError', 'True_', 'UFUNC_BUFSIZE_DEFAULT', 'UFUNC_PYVALS_NAME', 'VisibleDeprecationWarning', 'WRAP', '_NoValue', '__NUMPY_SETUP__', '__all__', '__builtins__', '__cached__', '__config__', '__doc__', '__file__', '__git_revision__', '__loader__', '__mkl_version__', '__name__', '__package__', '__path__', '__spec__', '__version__', '_distributor_init', '_globals', '_import_tools', '_mat', 'abs', 'absolute', 'absolute_import', 'add', 'add_docstring', 'add_newdoc', 'add_newdoc_ufunc', 'add_newdocs', 'alen', 'all', 'allclose', 'alltrue', 'amax', 'amin', 'angle', 'any', 'append', 'apply_along_axis', 'apply_over_axes', 'arange', 'arccos', 'arccosh', 'arcsin', 'arcsinh', 'arctan', 'arctan2', 'arctanh', 'argmax', 'argmin', 'argpartition', 'argsort', 'argwhere', 'around', 'array', 'array2string', 'array_equal', 'array_equiv', 'array_repr', 'array_split', 'array_str', 'asanyarray', 'asarray', 'asarray_chkfinite', 'ascontiguousarray', 'asfarray', 'asfortranarray', 'asmatrix', 'asscalar', 'atleast_1d', 'atleast_2d', 'atleast_3d', 'average', 'bartlett', 'base_repr', 'bench', 'binary_repr', 'bincount', 'bitwise_and', 'bitwise_not', 'bitwise_or', 'bitwise_xor', 'blackman', 'block', 'bmat', 'bool', 'bool8', 'bool_', 'broadcast', 'broadcast_arrays', 'broadcast_to', 'busday_count', 'busday_offset', 'busdaycalendar', 'byte', 'byte_bounds', 'bytes0', 'bytes_', 'c_', 'can_cast', 'cast', 'cbrt', 'cdouble', 'ceil', 'cfloat', 'char', 'character', 'chararray', 'choose', 'clip', 'clongdouble', 'clongfloat', 'column_stack', 'common_type', 'compare_chararrays', 'compat', 'complex', 'complex128', 'complex256', 'complex64', 'complex_', 'complexfloating', 'compress', 'concatenate', 'conj', 'conjugate', 'convolve', 'copy', 'copysign', 'copyto', 'core', 'corrcoef', 'correlate', 'cos', 'cosh', 'count_nonzero', 'cov', 'cross', 'csingle', 'ctypeslib', 'cumprod', 'cumproduct', 'cumsum', 'datetime64', 'datetime_as_string', 'datetime_data', 'deg2rad', 'degrees', 'delete', 'deprecate', 'deprecate_with_doc', 'diag', 'diag_indices', 'diag_indices_from', 'diagflat', 'diagonal', 'diff', 'digitize', 'disp', 'divide', 'division', 'divmod', 'dot', 'double', 'dsplit', 'dstack', 'dtype', 'e', 'ediff1d', 'einsum', 'einsum_path', 'emath', 'empty', 'empty_like', 'equal', 'errstate', 'euler_gamma', 'exp', 'exp2', 'expand_dims', 'expm1', 'extract', 'eye', 'fabs', 'fastCopyAndTranspose', 'fft', 'fill_diagonal', 'find_common_type', 'finfo', 'fix', 'flatiter', 'flatnonzero', 'flexible', 'flip', 'fliplr', 'flipud', 'float', 'float128', 'float16', 'float32', 'float64', 'float_', 'float_power', 'floating', 'floor', 'floor_divide', 'fmax', 'fmin', 'fmod', 'format_parser', 'frexp', 'frombuffer', 'fromfile', 'fromfunction', 'fromiter', 'frompyfunc', 'fromregex', 'fromstring', 'full', 'full_like', 'fv', 'generic', 'genfromtxt', 'geomspace', 'get_array_wrap', 'get_include', 'get_printoptions', 'getbufsize', 'geterr', 'geterrcall', 'geterrobj', 'gradient', 'greater', 'greater_equal', 'half', 'hamming', 'hanning', 'heaviside', 'histogram', 'histogram2d', 'histogramdd', 'hsplit', 'hstack', 'hypot', 'i0', 'identity', 'iinfo', 'imag', 'in1d', 'index_exp', 'indices', 'inexact', 'inf', 'info', 'infty', 'inner', 'insert', 'int', 'int0', 'int16', 'int32', 'int64', 'int8', 'int_', 'int_asbuffer', 'intc', 'integer', 'interp', 'intersect1d', 'intp', 'invert', 'ipmt', 'irr', 'is_busday', 'isclose', 'iscomplex', 'iscomplexobj', 'isfinite', 'isfortran', 'isin', 'isinf', 'isnan', 'isnat', 'isneginf', 'isposinf', 'isreal', 'isrealobj', 'isscalar', 'issctype', 'issubclass_', 'issubdtype', 'issubsctype', 'iterable', 'ix_', 'kaiser', 'kron', 'ldexp', 'left_shift', 'less', 'less_equal', 'lexsort', 'lib', 'linalg', 'linspace', 'little_endian', 'load', 'loads', 'loadtxt', 'log', 'log10', 'log1p', 'log2', 'logaddexp', 'logaddexp2', 'logical_and', 'logical_not', 'logical_or', 'logical_xor', 'logspace', 'long', 'longcomplex', 'longdouble', 'longfloat', 'longlong', 'lookfor', 'ma', 'mafromtxt', 'mask_indices', 'mat', 'math', 'matmul', 'matrix', 'matrixlib', 'max', 'maximum', 'maximum_sctype', 'may_share_memory', 'mean', 'median', 'memmap', 'meshgrid', 'mgrid', 'min', 'min_scalar_type', 'minimum', 'mintypecode', 'mirr', 'mod', 'modf', 'moveaxis', 'msort', 'multiply', 'nan', 'nan_to_num', 'nanargmax', 'nanargmin', 'nancumprod', 'nancumsum', 'nanmax', 'nanmean', 'nanmedian', 'nanmin', 'nanpercentile', 'nanprod', 'nanstd', 'nansum', 'nanvar', 'nbytes', 'ndarray', 'ndenumerate', 'ndfromtxt', 'ndim', 'ndindex', 'nditer', 'negative', 'nested_iters', 'newaxis', 'nextafter', 'nonzero', 'not_equal', 'nper', 'npv', 'numarray', 'number', 'obj2sctype', 'object', 'object0', 'object_', 'ogrid', 'oldnumeric', 'ones', 'ones_like', 'outer', 'packbits', 'pad', 'partition', 'percentile', 'pi', 'piecewise', 'pkgload', 'place', 'pmt', 'poly', 'poly1d', 'polyadd', 'polyder', 'polydiv', 'polyfit', 'polyint', 'polymul', 'polynomial', 'polysub', 'polyval', 'positive', 'power', 'ppmt', 'print_function', 'prod', 'product', 'promote_types', 'ptp', 'put', 'putmask', 'pv', 'r_', 'rad2deg', 'radians', 'random', 'rank', 'rate', 'ravel', 'ravel_multi_index', 'real', 'real_if_close', 'rec', 'recarray', 'recfromcsv', 'recfromtxt', 'reciprocal', 'record', 'remainder', 'repeat', 'require', 'reshape', 'resize', 'result_type', 'right_shift', 'rint', 'roll', 'rollaxis', 'roots', 'rot90', 'round', 'round_', 'row_stack', 's_', 'safe_eval', 'save', 'savetxt', 'savez', 'savez_compressed', 'sctype2char', 'sctypeDict', 'sctypeNA', 'sctypes', 'searchsorted', 'select', 'set_numeric_ops', 'set_printoptions', 'set_string_function', 'setbufsize', 'setdiff1d', 'seterr', 'seterrcall', 'seterrobj', 'setxor1d', 'shape', 'shares_memory', 'short', 'show_config', 'sign', 'signbit', 'signedinteger', 'sin', 'sinc', 'single', 'singlecomplex', 'sinh', 'size', 'sometrue', 'sort', 'sort_complex', 'source', 'spacing', 'split', 'sqrt', 'square', 'squeeze', 'stack', 'std', 'str', 'str0', 'str_', 'string_', 'subtract', 'sum', 'swapaxes', 'take', 'tan', 'tanh', 'tensordot', 'test', 'testing', 'tile', 'timedelta64', 'trace', 'tracemalloc_domain', 'transpose', 'trapz', 'tri', 'tril', 'tril_indices', 'tril_indices_from', 'trim_zeros', 'triu', 'triu_indices', 'triu_indices_from', 'true_divide', 'trunc', 'typeDict', 'typeNA', 'typecodes', 'typename', 'ubyte', 'ufunc', 'uint', 'uint0', 'uint16', 'uint32', 'uint64', 'uint8', 'uintc', 'uintp', 'ulonglong', 'unicode', 'unicode_', 'union1d', 'unique', 'unpackbits', 'unravel_index', 'unsignedinteger', 'unwrap', 'ushort', 'vander', 'var', 'vdot', 'vectorize', 'version', 'void', 'void0', 'vsplit', 'vstack', 'warnings', 'where', 'who', 'zeros', 'zeros_like']
In [3]:
Copied!
# find out what version we have
np.__version__
# find out what version we have
np.__version__
Out[3]:
'1.25.1'
The numpy documentation is crucial!
http://docs.scipy.org/doc/numpy/reference/
NDArrays¶
The core class is the numpy ndarray (n-dimensional array). The n-dimensional array object in NumPy is referred to as an ndarray, a multidimensional container of homogeneous items – i.e. all values in the array are the same type and size. These arrays can be one-dimensional (one row or column vector), two-dimensional (m rows x n columns), or three-dimensional (arrays within arrays).
Create array from a list¶
In [5]:
Copied!
# create an array from a list
a = np.array([9,0,2,1,0])
# create an array from a list
a = np.array([9,0,2,1,0])
In [6]:
Copied!
# find out the datatype
a.dtype
# find out the datatype
a.dtype
Out[6]:
dtype('int64')
In [7]:
Copied!
# find out the shape
a.shape
# find out the shape
a.shape
Out[7]:
(5,)
In [8]:
Copied!
# what is the shape
type(a.shape)
# what is the shape
type(a.shape)
Out[8]:
tuple
In [9]:
Copied!
# another array with a different datatype and shape
b = np.array([[5,3,1,9],[9,2,3,0]], dtype=np.float64)
# another array with a different datatype and shape
b = np.array([[5,3,1,9],[9,2,3,0]], dtype=np.float64)
In [98]:
Copied!
# array with 3 rows x 4 columns
a_2d = np.array([[3,2,0,1],[9,1,8,7],[4,0,1,6]])
a_2d
# array with 3 rows x 4 columns
a_2d = np.array([[3,2,0,1],[9,1,8,7],[4,0,1,6]])
a_2d
Out[98]:
array([[3, 2, 0, 1],
[9, 1, 8, 7],
[4, 0, 1, 6]])
In [99]:
Copied!
# check dtype and shape
b.dtype, b.shape
# check dtype and shape
b.dtype, b.shape
Out[99]:
(dtype('float64'), (2, 4))
Important Concept: The fastest varying dimension is the last dimension! The outer level of the hierarchy is the first dimension. (This is called "c-style" indexing)
Create arrays using functions¶
There are lots of ways to create arrays.
In [96]:
Copied!
# create some uniform arrays
c = np.zeros((9,9))
d = np.ones((3,6,3), dtype=np.complex128)
e = np.full((3,3), np.pi)
e = np.ones_like(c)
f = np.zeros_like(d)
#
g = np.random.rand(3,4)
# create some uniform arrays
c = np.zeros((9,9))
d = np.ones((3,6,3), dtype=np.complex128)
e = np.full((3,3), np.pi)
e = np.ones_like(c)
f = np.zeros_like(d)
#
g = np.random.rand(3,4)
The np.arange() function is used to generate an array with evenly spaced values within a given interval. np.arange() can be used with one, two, or three parameters to specify the start, stop, and step values. If only one value is passed to the function, it will be interpreted as the stop value:
In [12]:
Copied!
# create some ranges
np.arange(10)
# create some ranges
np.arange(10)
Out[12]:
array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
In [13]:
Copied!
# arange is left inclusive, right exclusive
np.arange(2,4,0.25)
# arange is left inclusive, right exclusive
np.arange(2,4,0.25)
Out[13]:
array([2. , 2.25, 2.5 , 2.75, 3. , 3.25, 3.5 , 3.75])
Similarly, the np.linspace() function is used to construct an array with evenly spaced numbers over a given interval. However, instead of the step parameter, np.linspace() takes a num parameter to specify the number of samples within the given interval:
In [14]:
Copied!
# linearly spaced
np.linspace(2,4,20)
# linearly spaced
np.linspace(2,4,20)
Out[14]:
array([2. , 2.10526316, 2.21052632, 2.31578947, 2.42105263,
2.52631579, 2.63157895, 2.73684211, 2.84210526, 2.94736842,
3.05263158, 3.15789474, 3.26315789, 3.36842105, 3.47368421,
3.57894737, 3.68421053, 3.78947368, 3.89473684, 4. ])
Note that unlike np.arange(), np.linspace() includes the stop value by default (this can be changed by passing endpoint=True). Finally, it should be noted that while we could have used np.arange() to generate the same array in the above example, it is recommended to use np.linspace() when a non-integer step (e.g. 0.25) is desired.
In [87]:
Copied!
np.linspace(2,4,20, endpoint = False)
np.linspace(2,4,20, endpoint = False)
Out[87]:
array([2. , 2.1, 2.2, 2.3, 2.4, 2.5, 2.6, 2.7, 2.8, 2.9, 3. , 3.1, 3.2,
3.3, 3.4, 3.5, 3.6, 3.7, 3.8, 3.9])
Create two-dimensional grids¶
In [3]:
Copied!
x = np.linspace(-4, 4, 9)
y = np.linspace(-5, 5, 11)
x_2d, y_2d = np.meshgrid(x, y)
x = np.linspace(-4, 4, 9)
y = np.linspace(-5, 5, 11)
x_2d, y_2d = np.meshgrid(x, y)
In [4]:
Copied!
x_2d
x_2d
Out[4]:
array([[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.],
[-4., -3., -2., -1., 0., 1., 2., 3., 4.]])
In [5]:
Copied!
y_2d
y_2d
Out[5]:
array([[-5., -5., -5., -5., -5., -5., -5., -5., -5.],
[-4., -4., -4., -4., -4., -4., -4., -4., -4.],
[-3., -3., -3., -3., -3., -3., -3., -3., -3.],
[-2., -2., -2., -2., -2., -2., -2., -2., -2.],
[-1., -1., -1., -1., -1., -1., -1., -1., -1.],
[ 0., 0., 0., 0., 0., 0., 0., 0., 0.],
[ 1., 1., 1., 1., 1., 1., 1., 1., 1.],
[ 2., 2., 2., 2., 2., 2., 2., 2., 2.],
[ 3., 3., 3., 3., 3., 3., 3., 3., 3.],
[ 4., 4., 4., 4., 4., 4., 4., 4., 4.],
[ 5., 5., 5., 5., 5., 5., 5., 5., 5.]])
Indexing¶
Basic indexing is similar to lists
In [7]:
Copied!
# get some individual elements of xx
x_2d[0,0], x_2d[-1,-1], x_2d[3,-5]
# get some individual elements of xx
x_2d[0,0], x_2d[-1,-1], x_2d[3,-5]
Out[7]:
(-4.0, 4.0, 0.0)
In [8]:
Copied!
# get some whole rows and columns
x_2d[0].shape, x_2d[:,-1].shape
# get some whole rows and columns
x_2d[0].shape, x_2d[:,-1].shape
Out[8]:
((9,), (11,))
In [9]:
Copied!
# get some ranges
x_2d[3:10,3:5].shape
# get some ranges
x_2d[3:10,3:5].shape
Out[9]:
(7, 2)
There are many advanced ways to index arrays. You can read about them in the manual. Here is one example.
In [10]:
Copied!
# use a boolean array as an index
idx = x_2d<0
x_2d[idx].shape
# use a boolean array as an index
idx = x_2d<0
x_2d[idx].shape
Out[10]:
(44,)
In [11]:
Copied!
# two dimensional grids
x = np.linspace(-2*np.pi, 2*np.pi, 100)
y = np.linspace(-np.pi, np.pi, 50)
xx, yy = np.meshgrid(x, y)
xx.shape, yy.shape
# two dimensional grids
x = np.linspace(-2*np.pi, 2*np.pi, 100)
y = np.linspace(-np.pi, np.pi, 50)
xx, yy = np.meshgrid(x, y)
xx.shape, yy.shape
Out[11]:
((50, 100), (50, 100))
In [12]:
Copied!
f = np.sin(xx) * np.cos(0.5*yy)
f = np.sin(xx) * np.cos(0.5*yy)
At this point you might be getting curious what these arrays "look" like. So we need to introduce some visualization.
In [7]:
Copied!
from matplotlib import pyplot as plt
# %matplotlib inline
from matplotlib import pyplot as plt
# %matplotlib inline
In [14]:
Copied!
plt.pcolormesh(f)
plt.pcolormesh(f)
Out[14]:
<matplotlib.collections.QuadMesh at 0x1143ebc10>
Manipulating array dimensions¶
In [15]:
Copied!
# transpose
plt.pcolormesh(f.T)
# transpose
plt.pcolormesh(f.T)
Out[15]:
<matplotlib.collections.QuadMesh at 0x11457d760>
In [16]:
Copied!
# Flip the array up/down (reverse the order of the rows)
plt.pcolormesh(np.flipud(f))
# Flip the array up/down (reverse the order of the rows)
plt.pcolormesh(np.flipud(f))
Out[16]:
<matplotlib.collections.QuadMesh at 0x1145e6e80>
In [17]:
Copied!
# reshape an array (wrong size)
g = np.reshape(f, (8,9))
# reshape an array (wrong size)
g = np.reshape(f, (8,9))
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) Cell In[17], line 2 1 # reshape an array (wrong size) ----> 2 g = np.reshape(f, (8,9)) File /opt/anaconda3/envs/research_computing_scipy/lib/python3.9/site-packages/numpy/core/fromnumeric.py:285, in reshape(a, newshape, order) 200 @array_function_dispatch(_reshape_dispatcher) 201 def reshape(a, newshape, order='C'): 202 """ 203 Gives a new shape to an array without changing its data. 204 (...) 283 [5, 6]]) 284 """ --> 285 return _wrapfunc(a, 'reshape', newshape, order=order) File /opt/anaconda3/envs/research_computing_scipy/lib/python3.9/site-packages/numpy/core/fromnumeric.py:59, in _wrapfunc(obj, method, *args, **kwds) 56 return _wrapit(obj, method, *args, **kwds) 58 try: ---> 59 return bound(*args, **kwds) 60 except TypeError: 61 # A TypeError occurs if the object does have such a method in its 62 # class, but its signature is not identical to that of NumPy's. This (...) 66 # Call _wrapit from within the except clause to ensure a potential 67 # exception has a traceback chain. 68 return _wrapit(obj, method, *args, **kwds) ValueError: cannot reshape array of size 5000 into shape (8,9)
In [18]:
Copied!
# reshape an array (right size) and mess it up
print(f.size)
g = np.reshape(f, (200,25))
plt.pcolormesh(g)
# reshape an array (right size) and mess it up
print(f.size)
g = np.reshape(f, (200,25))
plt.pcolormesh(g)
5000
Out[18]:
<matplotlib.collections.QuadMesh at 0x1147de760>
In [19]:
Copied!
f.shape
f.shape
Out[19]:
(50, 100)
In [20]:
Copied!
np.tile(f,(6,1)).shape
np.tile(f,(6,1)).shape
Out[20]:
(300, 100)
In [21]:
Copied!
# tile an array
plt.pcolormesh(np.tile(f,(6,1)))
# tile an array
plt.pcolormesh(np.tile(f,(6,1)))
Out[21]:
<matplotlib.collections.QuadMesh at 0x114948a60>
Broadcasting¶
Broadcasting is an efficient way to multiply arrays of different sizes
In [23]:
Copied!
from IPython.display import Image
Image(url='http://scipy-lectures.github.io/_images/numpy_broadcasting.png',
width=720)
from IPython.display import Image
Image(url='http://scipy-lectures.github.io/_images/numpy_broadcasting.png',
width=720)
Out[23]:
In [24]:
Copied!
# multiply f by x
print(f.shape, x.shape)
g = f * x
print(g.shape)
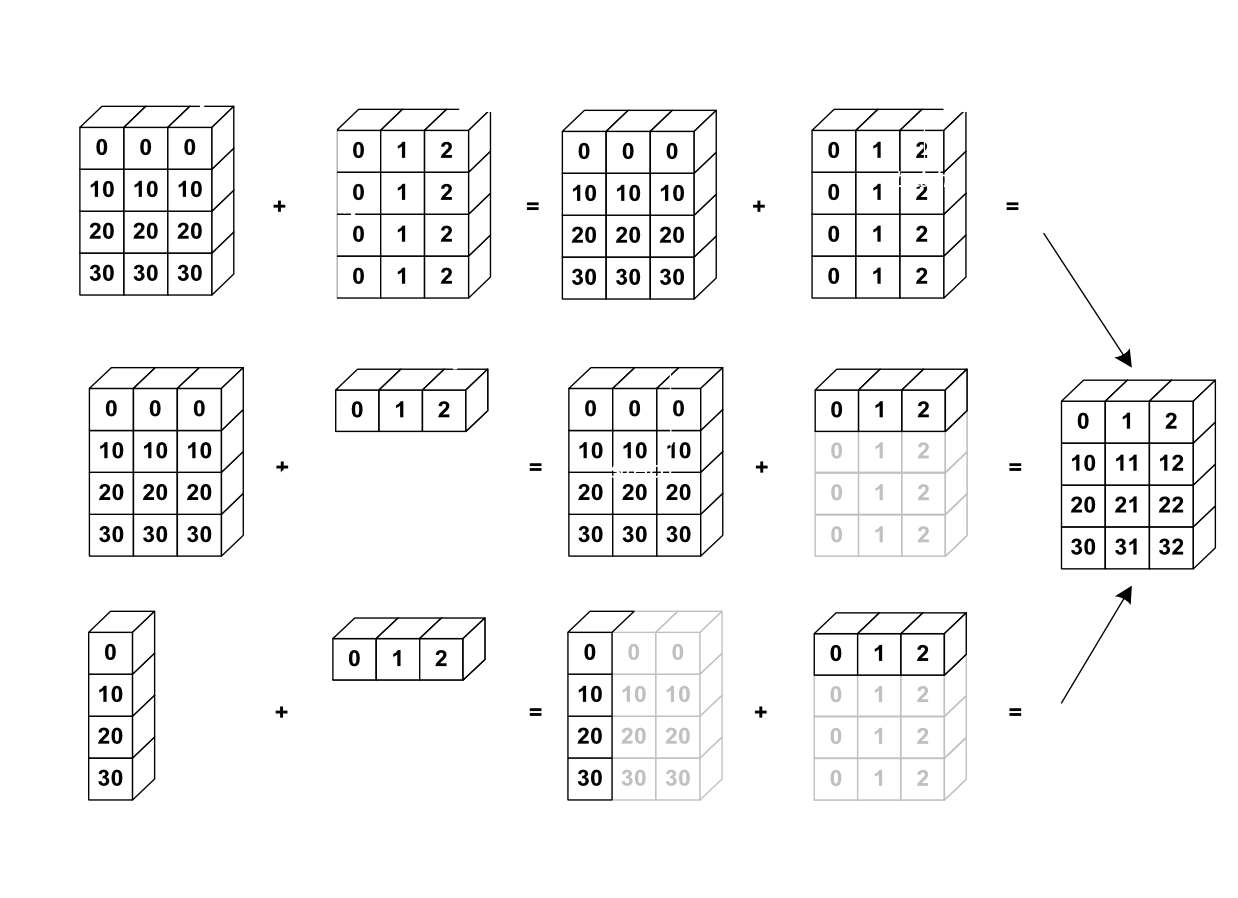
# multiply f by x
print(f.shape, x.shape)
g = f * x
print(g.shape)
(50, 100) (100,) (50, 100)
In [25]:
Copied!
# multiply f by y
print(f.shape, y.shape)
h = f * y
print(h.shape)
# multiply f by y
print(f.shape, y.shape)
h = f * y
print(h.shape)
(50, 100) (50,)
--------------------------------------------------------------------------- ValueError Traceback (most recent call last) Cell In[25], line 3 1 # multiply f by y 2 print(f.shape, y.shape) ----> 3 h = f * y 4 print(h.shape) ValueError: operands could not be broadcast together with shapes (50,100) (50,)
In [26]:
Copied!
# use newaxis special syntax
h = f * y[:,np.newaxis]
print(h.shape)
# use newaxis special syntax
h = f * y[:,np.newaxis]
print(h.shape)
(50, 100)
Reduction Operations¶
In [27]:
Copied!
# sum
g.sum()
# sum
g.sum()
Out[27]:
-3083.038387807155
In [28]:
Copied!
# mean
g.mean()
# mean
g.mean()
Out[28]:
-0.616607677561431
In [29]:
Copied!
# std
g.std()
# std
g.std()
Out[29]:
1.6402280119141424
In [30]:
Copied!
# apply on just one axis
# Mean of each row (calculated across columns)
g_xmean = g.mean(axis=1)
# Mean of each column (calculated across rows)
g_ymean = g.mean(axis=0)
# apply on just one axis
# Mean of each row (calculated across columns)
g_xmean = g.mean(axis=1)
# Mean of each column (calculated across rows)
g_ymean = g.mean(axis=0)
In [31]:
Copied!
plt.plot(x, g_ymean)
plt.plot(x, g_ymean)
Out[31]:
[<matplotlib.lines.Line2D at 0x114a38880>]
In [32]:
Copied!
plt.plot(g_xmean, y)
plt.plot(g_xmean, y)
Out[32]:
[<matplotlib.lines.Line2D at 0x114a8e6a0>]
Missing data¶
Most real-world datasets – environmental or otherwise – have data gaps. Data can be missing for any number of reasons, including observations not being recorded or data corruption. While a cell corresponding to a data gap may just be left blank in a spreadsheet, when imported into Python, there must be some way to handle "blank" or missing values.
Missing data should not be replaced with zeros, as 0 can be a valid value for many datasets, (e.g. temperature, precipitation, etc.). Instead, the convention is to fill all missing data with the constant NaN. NaN stands for "Not a Number" and is implemented in NumPy as np.nan.
NaNs are handled differently by different packages. In NumPy, all computations involving NaN values will return nan:
In [33]:
Copied!
data = np.array([[2.,2.7,1.89],
[1.1, 0.0, np.nan],
[3.2, 0.74, 2.1]])
data = np.array([[2.,2.7,1.89],
[1.1, 0.0, np.nan],
[3.2, 0.74, 2.1]])
In [34]:
Copied!
np.mean(data)
np.mean(data)
Out[34]:
nan
In [35]:
Copied!
np.nanmean(data)
np.nanmean(data)
Out[35]:
1.71625
More Matplotlib¶
Figure and Axes¶
The figure is the highest level of organization of matplotlib objects. If we want, we can create a figure explicitly.
In [36]:
Copied!
fig = plt.figure()
fig = plt.figure()
<Figure size 640x480 with 0 Axes>
In [37]:
Copied!
fig = plt.figure(figsize=(13, 5))
fig = plt.figure(figsize=(13, 5))
<Figure size 1300x500 with 0 Axes>
In [38]:
Copied!
fig = plt.figure()
ax = fig.add_axes([0, 0, 1, 1])
fig = plt.figure()
ax = fig.add_axes([0, 0, 1, 1])
In [39]:
Copied!
fig = plt.figure()
ax = fig.add_axes([0, 0, 0.5, 1])
fig = plt.figure()
ax = fig.add_axes([0, 0, 0.5, 1])
In [40]:
Copied!
fig = plt.figure()
ax1 = fig.add_axes([0, 0, 0.5, 1])
ax2 = fig.add_axes([0.6, 0, 0.3, 0.5], facecolor='g')
fig = plt.figure()
ax1 = fig.add_axes([0, 0, 0.5, 1])
ax2 = fig.add_axes([0.6, 0, 0.3, 0.5], facecolor='g')
Subplots¶
Subplot syntax is one way to specify the creation of multiple axes.
In [41]:
Copied!
fig = plt.figure()
axes = fig.subplots(nrows=2, ncols=3)
fig = plt.figure()
axes = fig.subplots(nrows=2, ncols=3)
In [43]:
Copied!
fig = plt.figure(figsize=(12, 6))
axes = fig.subplots(nrows=2, ncols=3)
fig = plt.figure(figsize=(12, 6))
axes = fig.subplots(nrows=2, ncols=3)
In [44]:
Copied!
axes
axes
Out[44]:
array([[<Axes: >, <Axes: >, <Axes: >],
[<Axes: >, <Axes: >, <Axes: >]], dtype=object)
There is a shorthand for doing this all at once.
This is our recommended way to create new figures!
In [45]:
Copied!
fig, ax = plt.subplots()
fig, ax = plt.subplots()
In [46]:
Copied!
ax
ax
Out[46]:
<Axes: >
In [47]:
Copied!
fig, axes = plt.subplots(ncols=2, figsize=(8, 4), subplot_kw={'facecolor': 'g'})
fig, axes = plt.subplots(ncols=2, figsize=(8, 4), subplot_kw={'facecolor': 'g'})
In [48]:
Copied!
axes
axes
Out[48]:
array([<Axes: >, <Axes: >], dtype=object)
Drawing into Axes¶
All plots are drawn into axes. It is easiest to understand how matplotlib works if you use the object-oriented style.
In [49]:
Copied!
# create some data to plot
import numpy as np
x = np.linspace(-np.pi, np.pi, 100)
y = np.cos(x)
z = np.sin(6*x)
# create some data to plot
import numpy as np
x = np.linspace(-np.pi, np.pi, 100)
y = np.cos(x)
z = np.sin(6*x)
In [50]:
Copied!
fig, ax = plt.subplots()
ax.plot(x, y)
fig, ax = plt.subplots()
ax.plot(x, y)
Out[50]:
[<matplotlib.lines.Line2D at 0x114ca27c0>]
This does the same thing as
In [51]:
Copied!
plt.plot(x, y)
plt.plot(x, y)
Out[51]:
[<matplotlib.lines.Line2D at 0x173539e80>]
This starts to matter when we have multiple axes to worry about.
In [52]:
Copied!
fig, axes = plt.subplots(figsize=(8, 4), ncols=2)
ax0, ax1 = axes
ax0.plot(x, y)
ax1.plot(x, z)
fig, axes = plt.subplots(figsize=(8, 4), ncols=2)
ax0, ax1 = axes
ax0.plot(x, y)
ax1.plot(x, z)
Out[52]:
[<matplotlib.lines.Line2D at 0x1736068e0>]
Labeling Plots¶
In [53]:
Copied!
fig, axes = plt.subplots(figsize=(8, 4), ncols=2)
ax0, ax1 = axes
ax0.plot(x, y)
ax0.set_xlabel('x')
ax0.set_ylabel('y')
ax0.set_title('x vs. y')
ax1.plot(x, z)
ax1.set_xlabel('x')
ax1.set_ylabel('z')
ax1.set_title('x vs. z')
# squeeze everything in
plt.tight_layout()
fig, axes = plt.subplots(figsize=(8, 4), ncols=2)
ax0, ax1 = axes
ax0.plot(x, y)
ax0.set_xlabel('x')
ax0.set_ylabel('y')
ax0.set_title('x vs. y')
ax1.plot(x, z)
ax1.set_xlabel('x')
ax1.set_ylabel('z')
ax1.set_title('x vs. z')
# squeeze everything in
plt.tight_layout()
Customizing Line Plots¶
In [54]:
Copied!
fig, ax = plt.subplots()
ax.plot(x, y, x, z)
fig, ax = plt.subplots()
ax.plot(x, y, x, z)
Out[54]:
[<matplotlib.lines.Line2D at 0x1737b42e0>, <matplotlib.lines.Line2D at 0x1737b4340>]
It's simple to switch axes
In [55]:
Copied!
fig, ax = plt.subplots()
ax.plot(y, x, z, x)
fig, ax = plt.subplots()
ax.plot(y, x, z, x)
Out[55]:
[<matplotlib.lines.Line2D at 0x173839670>, <matplotlib.lines.Line2D at 0x1738396d0>]
Line Styles¶
In [56]:
Copied!
fig, axes = plt.subplots(figsize=(16, 5), ncols=3)
axes[0].plot(x, y, linestyle='dashed')
axes[0].plot(x, z, linestyle='--')
axes[1].plot(x, y, linestyle='dotted')
axes[1].plot(x, z, linestyle=':')
axes[2].plot(x, y, linestyle='dashdot', linewidth=5)
axes[2].plot(x, z, linestyle='-.', linewidth=0.5)
fig, axes = plt.subplots(figsize=(16, 5), ncols=3)
axes[0].plot(x, y, linestyle='dashed')
axes[0].plot(x, z, linestyle='--')
axes[1].plot(x, y, linestyle='dotted')
axes[1].plot(x, z, linestyle=':')
axes[2].plot(x, y, linestyle='dashdot', linewidth=5)
axes[2].plot(x, z, linestyle='-.', linewidth=0.5)
Out[56]:
[<matplotlib.lines.Line2D at 0x1739476d0>]
Colors¶
As described in the colors documentation, there are some special codes for commonly used colors:
- b: blue
- g: green
- r: red
- c: cyan
- m: magenta
- y: yellow
- k: black
- w: white
In [57]:
Copied!
fig, ax = plt.subplots()
ax.plot(x, y, color='k')
ax.plot(x, z, color='r')
fig, ax = plt.subplots()
ax.plot(x, y, color='k')
ax.plot(x, z, color='r')
Out[57]:
[<matplotlib.lines.Line2D at 0x173a47850>]
Other ways to specify colors:
In [58]:
Copied!
fig, axes = plt.subplots(figsize=(16, 5), ncols=3)
# grayscale
axes[0].plot(x, y, color='0.8')
axes[0].plot(x, z, color='0.2')
# RGB tuple
axes[1].plot(x, y, color=(1, 0, 0.7))
axes[1].plot(x, z, color=(0, 0.4, 0.3))
# HTML hex code
axes[2].plot(x, y, color='#00dcba')
axes[2].plot(x, z, color='#b029ee')
fig, axes = plt.subplots(figsize=(16, 5), ncols=3)
# grayscale
axes[0].plot(x, y, color='0.8')
axes[0].plot(x, z, color='0.2')
# RGB tuple
axes[1].plot(x, y, color=(1, 0, 0.7))
axes[1].plot(x, z, color=(0, 0.4, 0.3))
# HTML hex code
axes[2].plot(x, y, color='#00dcba')
axes[2].plot(x, z, color='#b029ee')
Out[58]:
[<matplotlib.lines.Line2D at 0x173b536d0>]
There is a default color cycle built into matplotlib.
In [59]:
Copied!
plt.rcParams['axes.prop_cycle']
plt.rcParams['axes.prop_cycle']
Out[59]:
| 'color' |
|---|
| '#1f77b4' |
| '#ff7f0e' |
| '#2ca02c' |
| '#d62728' |
| '#9467bd' |
| '#8c564b' |
| '#e377c2' |
| '#7f7f7f' |
| '#bcbd22' |
| '#17becf' |
In [60]:
Copied!
fig, ax = plt.subplots(figsize=(12, 10))
for factor in np.linspace(0.2, 1, 11):
ax.plot(x, factor*y)
fig, ax = plt.subplots(figsize=(12, 10))
for factor in np.linspace(0.2, 1, 11):
ax.plot(x, factor*y)
Markers¶
There are lots of different markers availabile in matplotlib!
In [61]:
Copied!
fig, axes = plt.subplots(figsize=(12, 5), ncols=2)
axes[0].plot(x[:20], y[:20], marker='.')
axes[0].plot(x[:20], z[:20], marker='o')
axes[1].plot(x[:20], z[:20], marker='^',
markersize=10, markerfacecolor='r',
markeredgecolor='k')
fig, axes = plt.subplots(figsize=(12, 5), ncols=2)
axes[0].plot(x[:20], y[:20], marker='.')
axes[0].plot(x[:20], z[:20], marker='o')
axes[1].plot(x[:20], z[:20], marker='^',
markersize=10, markerfacecolor='r',
markeredgecolor='k')
Out[61]:
[<matplotlib.lines.Line2D at 0x114e7e310>]
Label, Ticks, and Gridlines¶
In [73]:
Copied!
fig, ax = plt.subplots(figsize=(12, 7))
ax.plot(x, y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('A complicated math function: $f(x) = \cos(x)$')
ax.set_xticks(np.pi * np.array([-1, 0, 1]))
ax.set_xticklabels(['$-\pi$', '0', '$\pi$'])
ax.set_yticks([-1, 0, 1])
ax.set_yticks(np.arange(-1, 1.1, 0.2), minor=True)
#ax.set_xticks(np.arange(-3, 3.1, 0.2), minor=True)
ax.grid(which='minor', linestyle='--')
ax.grid(which='major', linewidth=2)
fig, ax = plt.subplots(figsize=(12, 7))
ax.plot(x, y)
ax.set_xlabel('x')
ax.set_ylabel('y')
ax.set_title('A complicated math function: $f(x) = \cos(x)$')
ax.set_xticks(np.pi * np.array([-1, 0, 1]))
ax.set_xticklabels(['$-\pi$', '0', '$\pi$'])
ax.set_yticks([-1, 0, 1])
ax.set_yticks(np.arange(-1, 1.1, 0.2), minor=True)
#ax.set_xticks(np.arange(-3, 3.1, 0.2), minor=True)
ax.grid(which='minor', linestyle='--')
ax.grid(which='major', linewidth=2)
Axis Limits¶
In [63]:
Copied!
fig, ax = plt.subplots()
ax.plot(x, y, x, z)
ax.set_xlim(-5, 5)
ax.set_ylim(-3, 3)
fig, ax = plt.subplots()
ax.plot(x, y, x, z)
ax.set_xlim(-5, 5)
ax.set_ylim(-3, 3)
Out[63]:
(-3.0, 3.0)
In [64]:
Copied!
fig, ax = plt.subplots()
ax.plot(x, y, x, z)
ax.set_xlim(-5, 5)
ax.set_ylim(-100, 100)
fig, ax = plt.subplots()
ax.plot(x, y, x, z)
ax.set_xlim(-5, 5)
ax.set_ylim(-100, 100)
Out[64]:
(-100.0, 100.0)
Text Annotations¶
In [65]:
Copied!
fig, ax = plt.subplots()
ax.plot(x, y)
ax.text(-3, 0.3, 'hello world')
ax.annotate('the maximum', xy=(0, 1),
xytext=(0, 0), arrowprops={'facecolor': 'k'})
fig, ax = plt.subplots()
ax.plot(x, y)
ax.text(-3, 0.3, 'hello world')
ax.annotate('the maximum', xy=(0, 1),
xytext=(0, 0), arrowprops={'facecolor': 'k'})
Out[65]:
Text(0, 0, 'the maximum')
In [78]:
Copied!
fig, ax = plt.subplots()
ax.plot(x, y)
ax.text(0.1, 0.9, 'hello world', transform=ax.transAxes)
ax.annotate('the maximum', xy=(0, 1),
xytext=(0, 0), arrowprops={'facecolor': 'k'})
fig, ax = plt.subplots()
ax.plot(x, y)
ax.text(0.1, 0.9, 'hello world', transform=ax.transAxes)
ax.annotate('the maximum', xy=(0, 1),
xytext=(0, 0), arrowprops={'facecolor': 'k'})
Out[78]:
Text(0, 0, 'the maximum')
In [66]:
Copied!
fig, ax = plt.subplots()
splot = ax.scatter(y, z, c=x, s=(100*z**2 + 5))
fig.colorbar(splot)
fig, ax = plt.subplots()
splot = ax.scatter(y, z, c=x, s=(100*z**2 + 5))
fig.colorbar(splot)
Out[66]:
<matplotlib.colorbar.Colorbar at 0x173e08af0>
Bar Plots¶
In [67]:
Copied!
labels = ['first', 'second', 'third']
values = [10, 5, 30]
fig, axes = plt.subplots(figsize=(10, 5), ncols=2)
axes[0].bar(labels, values)
axes[1].barh(labels, values)
labels = ['first', 'second', 'third']
values = [10, 5, 30]
fig, axes = plt.subplots(figsize=(10, 5), ncols=2)
axes[0].bar(labels, values)
axes[1].barh(labels, values)
Out[67]:
<BarContainer object of 3 artists>
In [ ]:
Copied!
In [5]:
Copied!
x1d = np.linspace(-2*np.pi, 2*np.pi, 100)
y1d = np.linspace(-np.pi, np.pi, 50)
xx, yy = np.meshgrid(x1d, y1d)
f = np.cos(xx) * np.sin(yy)
print(f.shape)
x1d = np.linspace(-2*np.pi, 2*np.pi, 100)
y1d = np.linspace(-np.pi, np.pi, 50)
xx, yy = np.meshgrid(x1d, y1d)
f = np.cos(xx) * np.sin(yy)
print(f.shape)
(50, 100)
In [8]:
Copied!
fig, ax = plt.subplots(figsize=(12,4), ncols=2)
ax[0].imshow(f)
ax[1].imshow(f, origin='lower')
fig, ax = plt.subplots(figsize=(12,4), ncols=2)
ax[0].imshow(f)
ax[1].imshow(f, origin='lower')
Out[8]:
<matplotlib.image.AxesImage at 0x10c79f3d0>
pcolormesh¶
In [9]:
Copied!
fig, ax = plt.subplots(ncols=2, figsize=(12, 5))
pc0 = ax[0].pcolormesh(x1d, y1d, f)
pc1 = ax[1].pcolormesh(xx, yy, f)
fig.colorbar(pc0, ax=ax[0])
fig.colorbar(pc1, ax=ax[1])
fig, ax = plt.subplots(ncols=2, figsize=(12, 5))
pc0 = ax[0].pcolormesh(x1d, y1d, f)
pc1 = ax[1].pcolormesh(xx, yy, f)
fig.colorbar(pc0, ax=ax[0])
fig.colorbar(pc1, ax=ax[1])
Out[9]:
<matplotlib.colorbar.Colorbar at 0x10c9d2e20>
In [13]:
Copied!
x_sm, y_sm, f_sm = xx[:10, :10], yy[:10, :10], f[:10, :10]
fig, ax = plt.subplots(figsize=(12,5), ncols=2)
# last row and column ignored!
ax[0].pcolormesh(x_sm, y_sm, f_sm, edgecolors='k', shading = 'nearest')
# same!
ax[1].pcolormesh(x_sm, y_sm, f_sm[:-1, :-1], edgecolors='k', shading = 'flat')
x_sm, y_sm, f_sm = xx[:10, :10], yy[:10, :10], f[:10, :10]
fig, ax = plt.subplots(figsize=(12,5), ncols=2)
# last row and column ignored!
ax[0].pcolormesh(x_sm, y_sm, f_sm, edgecolors='k', shading = 'nearest')
# same!
ax[1].pcolormesh(x_sm, y_sm, f_sm[:-1, :-1], edgecolors='k', shading = 'flat')
Out[13]:
<matplotlib.collections.QuadMesh at 0x10d8555b0>
In [ ]:
Copied!